数组&字符串

416. 划分为2个相等的子集⭐

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

本题是经典的「NP 完全问题」，即多项式复杂程度的非确定性问题。

1. 0-1背包

#dp[i][j] 表示从数组 [0,i] 内是否存在和为 j

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        n = len(nums)
        if n < 2: return False

        total = sum(nums)
        target = total//2
        if total % 2: return False
        if max(nums) > target: return False

        dp = [[False]*(target+1) for _ in range(n)]
        for i in range(n):
            dp[i][0] = True
        dp[0][nums[0]] = True

        for i in range(1, n):
            num = nums[i]
            for j in range(1,target+1):
                if j>=num:
                    dp[i][j] = dp[i-1][j] | dp[i-1][j-num]
                else:
                    dp[i][j] = dp[i-1][j]
        
        return dp[-1][-1]

空间优化之后：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        n = len(nums)
        if n < 2: return False

        total = sum(nums)
        target = total//2
        if total % 2: return False
        if max(nums) > target: return False

        dp = [False]*(target+1)
        dp[0] = True

        for i, num in enumerate(nums):
            for j in range(target, num-1, -1):
                dp[j] |= dp[j-num]
        return dp[target]

# 第二层循环需要从大到小计算
# 这样子，dp[j-num] 总是未更新的值

698. 划分为k个相等的子集⭐

1. 回溯

class Solution:
    def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
        if k == 1: return True
        if sum(nums) % k: return False 
        target = sum(nums)//k
        nums.sort()                  #贪心
        if nums[0]>target: return False

        while nums and nums[-1]==target:
            nums.pop()
            k-=1 
        if not nums: return True

        def dfs(need,nums):
            if not nums: return True
            val = nums[-1]
            for i in range(k):
                if val <= need[i]:
                    need[i] -= val
                    if dfs(need, nums[:-1]):
                        return True
                    need[i] += val
                if need[i]==target:  #剪枝，不懂，测试时优化了好多
                    break
            return False
        return dfs([target]*k,nums)

253. 会议室 II⭐

给你一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，为避免会议冲突，同时要考虑充分利用会议室资源，请你计算至少需要多少间会议室，才能满足这些会议安排。

1. 排序 + 最小堆

from heapq import *
class Solution:
    def minMeetingRooms(self, intervals: List[List[int]]) -> int:
        if not intervals: return 0
        intervals.sort()

        heap = [intervals[0][1]]
        for begin,end in intervals[1:]:
            if heap[0] <= begin:
                heappop(heap)
            heappush(heap, end)
        return len(heap)

经典，没学过的完全不会

2. 当成上下车来做

取 intervals = [[0,30],[5,10],[15,20]] 进行分析，
第一个人从0上车，从30下车；
第二个人从5上车，10下车。。。

我们的问题转化为最多车上有几个人（也就是最多有多少会议室）。

容易理解的版本：

class Solution:
    def minMeetingRooms(self, intervals: List[List[int]]) -> int:
        if not intervals: return 0

        res = 0
        n = len(intervals)
        begin = sorted([i[0] for i in intervals])
        end = sorted([i[1] for i in intervals])

        cnt = 0
        p_add, p_sub = 0, 0
        for p_add in range(n):
            while p_sub < n and  end[p_sub]<=begin[p_add]:
                p_sub += 1
                cnt -= 1
            cnt += 1
            res = max(res, cnt)
        return res

化简后：

class Solution:
    def minMeetingRooms(self, intervals: List[List[int]]) -> int:
        if not intervals: return 0

        res = 0
        n = len(intervals)
        begin = sorted([i[0] for i in intervals])
        end = sorted([i[1] for i in intervals])

        p_add, p_sub = 0, 0
        for p_add in range(n):
            if end[p_sub] <= begin[p_add]:
                p_sub += 1
                res -= 1
            res += 1
        return res

218. 天际线问题

遍历改变的点，维护一个高度的队列

#相同的x坐标先算 坐标为左坐标的 那个 h，所以changes.append((l, -h))
from sortedcontainers import SortedList

class Solution:
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        res = []
        changes = []
        for l, r, h in buildings:
            changes.append((l, -h))
            changes.append((r, h))
        changes.sort()

        lives = SortedList([0])
        pre = 0

        for x, h in changes:  # 对每个高度可能改变的点遍历
            if h < 0:
                lives.add(h)
            else:
                lives.remove(-h)
            
            cur = lives[0]  #当前最高的高度的负值
            if cur != pre:
                res.append([x, -cur])
            pre = cur

        return res

169. 多数元素

投票算法

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        cnt, pre = 0, None
        for num in nums:
            if not cnt:
                pre = num
            cnt += (1 if num==pre else -1)
        return pre

75. 颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

#荷兰国旗问题，快速排序基础
class Solution:
    def sortColors(self, nums: List[int]) -> None:
        i, l, r=0, 0, len(nums)-1
        while i <= r:
            if nums[i] == 0:
                nums[i], nums[l] = nums[l], nums[i]
                l += 1
                i += 1
            elif nums[i] == 2:
                nums[i], nums[r] = nums[r], nums[i]
                r -= 1
            else: i += 1

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        map={'2':"abc",'3':"def",'4':"ghi",'5':"jkl",'6':"mno",'7':"pqrs",'8':"tuv",'9':"wxyz"}
        if not digits: return []
        ans=[""]
        for i in digits:
            ans=[pre+suf for pre in ans for suf in map[i]]
        return ans

696.计数二进制子串

给定一个字符串 s，计算具有相同数量0和1的非空(连续)子字符串的数量，并且这些子字符串中的所有0和所有1都是组合在一起的。

重复出现的子串要计算它们出现的次数。

class Solution:
    def countBinarySubstrings(self, s: str) -> int:
        temp=[1]
        ans=0
        for i in range(1,len(s)):
            if s[i]==s[i-1]:
                temp[-1]+=1
            else:
                temp.append(1)
        for i in range(len(temp)-1):
            ans+=min(temp[i],temp[i+1])
        return ans

# 计算相邻数的频数
# 看着有些抽象

605.种花问题

假设你有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花卉不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给定一个花坛（表示为一个数组包含0和1，其中0表示没种植花，1表示种植了花），和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花？能则返回True，不能则返回False。

class Solution:
    def canPlaceFlowers(self, f: List[int], n: int) -> bool:
        f=[0]+f+[0,1]
        ans,cnt=0,0
        for i in f:
            if i==0: cnt+=1
            else: 
                ans+=(cnt-1)//2
                cnt=0
        #print(ans,n)
        return ans>=n

# 数组，两端加值便于解题。

74.搜索二维矩阵

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

• 每行中的整数从左到右按升序排列。
• 每行的第一个整数大于前一行的最后一个整数。

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        rows,cols=len(matrix),len(matrix[0])
        l,r=0,rows*cols-1
        while l<=r:
            mid=(l+r)//2
            x,y=mid//cols,mid%cols
            if matrix[x][y]==target: return True
            elif matrix[x][y]>target: r=mid-1
            else: l=mid+1
        return False

#原地二分查找

852.山脉数组的峰顶索引

class Solution:
    def peakIndexInMountainArray(self, arr: List[int]) -> int:
        l, r = 0, len(arr)-1
        while l<r:
            mid = (l+r)//2
            if arr[mid] > arr[mid+1]:
                r = mid
            else:
                l = mid + 1
        return l

#二分的变式

287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，找出 这个重复的数 。

你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

1. 快慢指针

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        slow, fast = nums[0], nums[nums[0]]
        while slow != fast:
            slow = nums[slow]
            fast = nums[nums[fast]]
        slow = 0
        while slow != fast:
            slow = nums[slow]
            fast = nums[fast]
        return slow

# 看成链表，Floyd判圈算法

2. 二分查找

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        l, r = 1, len(nums)
        while l<r:
            mid = (l+r)//2
            cnt = sum([num<=mid for num in nums])
            if cnt <= mid:
                l = mid + 1
            else:
                r = mid
        return r
# 时间复杂度：O(nlogn)

kmp算法

kmp是一个效率非常高的字符串匹配算法。
有问题如下：

#求b在a中出现次数
a = "ababacababadababadadda"
b = "ababad"

kmp可以将暴力法的O(m*n)降低为O(m+n)

过程:
1. 计算temp数组
temp数组可理解为一组b中相同前后缀的标记(不能为本身长度)

b = "ababad"
对第一位'a'，没有相同前后缀，temp[0] = 0
对第二位'ab'，temp[1] = 0
对第三位’aba'，temp[2] = 1
以此类推，temp= [0,0,1,2,3,0]

def cal_temp(b):
    #K是一个对相同前后缀的标记
    temp,k=[0],0
    #从索引1处开始遍历
    for i in range(1,len(b)):
        while k>0 and b[i]!=b[k]:
            k=temp[k-1]
        if b[i]==b[k]:
            k+=1
        temp.append(k)
    return temp

分析一下代码：

• i=1时，’ab’，b[1]!=b[0]，temp.append(0)
• i=2时，’aba’，b[2]==b[0]，temp.append(1)
• i=3时，’abab’，b[3]==b[1]，temp.append(2)
• i=4时，’ababa’，b[4]==b[2]，temp.append(3)
• i=5时，’ababad’，temp=[0,0,1,2,3]
  b[5]!=b[3]，k=temp[3-1]=1
  b[5]!=b[1]，k=temp[1-1]=0
  temp.append(0)

发现比较难理解的是那个回溯的地方：k=temp[k-1]
没事，把i=5的情况再分析一下：

i=5时，’ababad’，temp=[0,0,1,2,3]，k=3

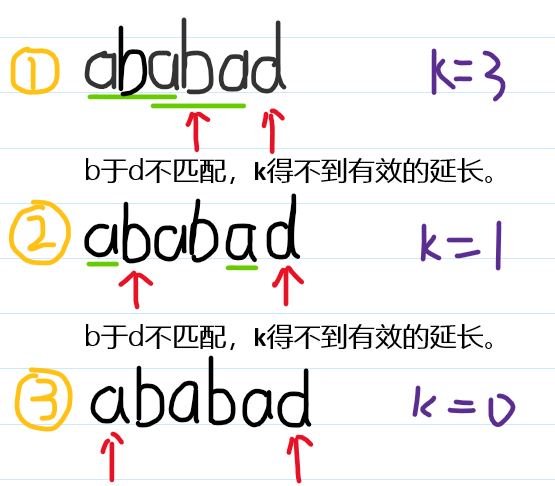
aba and aba can match,k=3
a and a can match,k=(aba的匹配数1,即temp[k-1])
more explain: aba can see as a and a,the first a can match the fourth a

2. kmp
打完上面的怪，就可以直接写kmp了

def kmp(a,b):
    temp=cal_temp(b)
    ans,k=0,0
    for i in range(len(a)):
        while k>0 and a[i]!=b[k]:
            k=temp[k-1]
        if a[i]==b[k]:
            k+=1
        if k==len(b):
            ans+=1
            k=temp[k-1]
    return ａｎｓ

#小结：利用已匹配的信息，迈出比较大的步子。