preface
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就 “回溯” 返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。
代码框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
参考博客:
leetcode题目:https://leetcode-cn.com/tag/backtracking/
77. 组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
1. itertools 库
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
return list(itertools.combinations(range(1,n+1),k))
2. 回溯
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
ans=[]
def bk(n,k,tmp,start):
if len(tmp)==k:
ans.append(tmp[:])
return
for i in range(start,n+1):
tmp.append(i)
bk(n,k,tmp,i+1)
tmp.pop()
bk(n,k,[],1)
return ans
46. 全排列
1. itertools 库
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
return list(itertools.permutations(nums))
2. 回溯
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
ans = []
def bk(tmp, use):
if not use:
ans.append(tmp[:])
return
for i,idx in enumerate(use):
tmp.append(nums[idx])
bk(tmp,use[:i]+use[i+1:])
tmp.pop()
bk([],list(range(len(nums))))
return ans
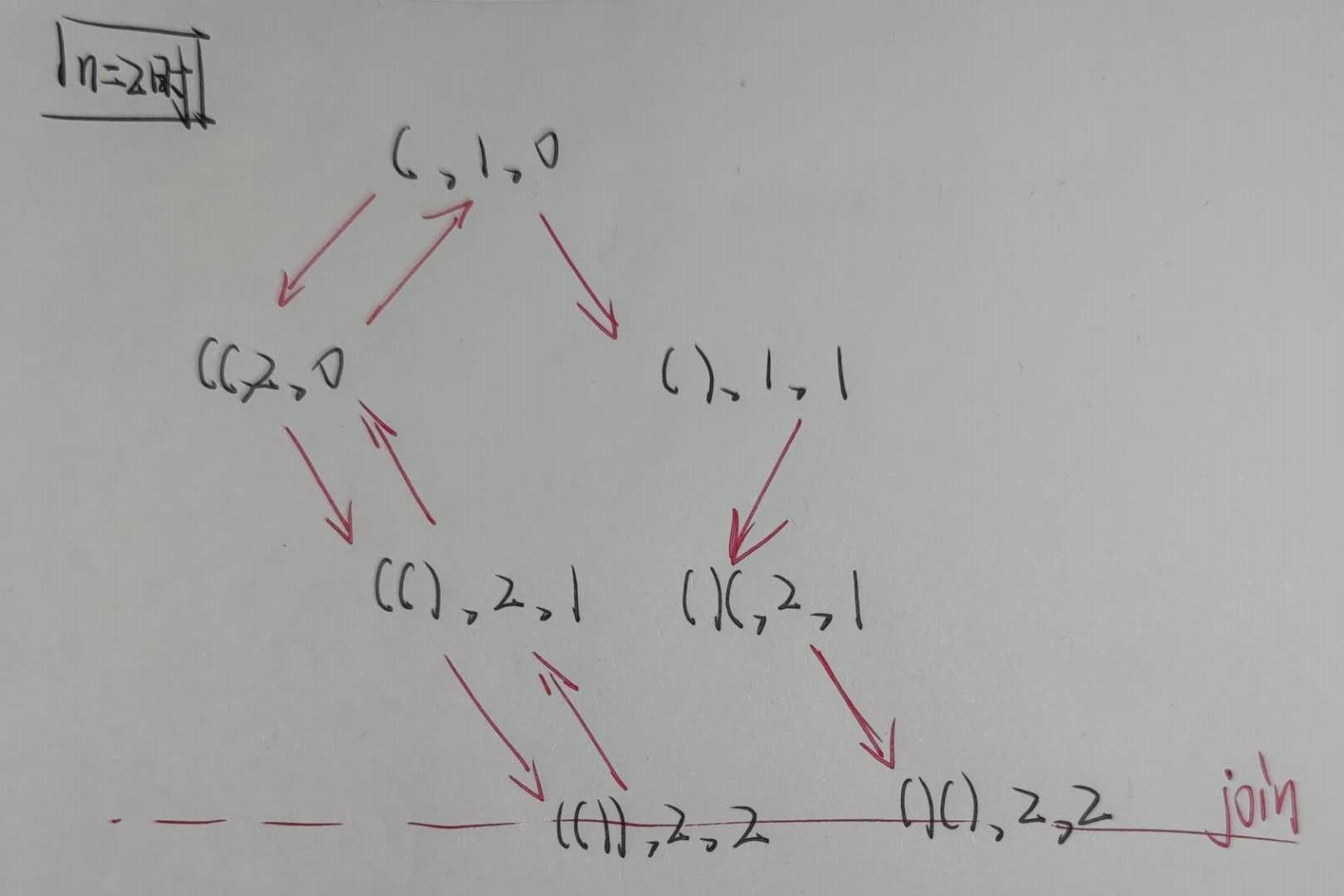
(1)22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
ans=[]
def backtrack(s,l,r): #s表cur_str_list,l 表示左括号数
if len(s)==2*n:
ans.append(''.join(s))
return
if l<n:
s.append('(')
backtrack(s,l+1,r)
s.pop()
if r<l:
s.append(')')
backtrack(s,l,r+1)
s.pop()
backtrack([],0,0)
return ans
(2)无重复字符串的排列组合
无重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合,字符串每个字符均不相同。
# 方法一:用itertools库中的permutations
return [''.join(i) for i in list(permutations(S))]
#方法二:回溯
class Solution:
def permutation(self, S: str) -> List[str]:
if not S: return []
ans=[]
def backtrack(s,path,ans):
if not s:
ans.append(path)
return
for i in range(len(s)):
backtrack(s[:i]+s[i+1:],path+s[i],ans)
backtrack(S,'',ans)
return ans
(3)幂集
编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
输入: nums = [1,2,3]
输出:[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]]
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ans=[]
#l表示可取的左点,r表示可取的右点
def backtrack(ans,subset,l,r):
ans.append(subset[:])
for i in range(l,r):
subset.append(nums[i])
backtrack(ans,subset,i+1,r)
subset.pop()
backtrack(ans,[],0,len(nums))
return ans
#回溯法厉害啊,2020-9-13的第三道回溯
#这代码应该可以叫模板了
(4)八皇后问题
https://leetcode-cn.com/problems/eight-queens-lcci/
设计一种算法,打印 N 皇后在 N × N 棋盘上的各种摆法,其中每个皇后都不同行、不同列,也不在对角线上。这里的“对角线”指的是所有的对角线,不只是平分整个棋盘的那两条对角线。
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
ans=[]
def queen(A, cur=0):
if cur == len(A):
ans.append(A[:])
return
for i in range(len(A)):
A[cur] = i
flag = True
#检验与前面的皇后是否冲突
for j in range(cur):
if A[j]==i or abs(i - A[j]) == cur - j:
flag = False
break
if flag: queen(A, cur+1)
queen([None]*n)
#接口对接部分
temp=[[['.' for _ in range(n)] for _ in range(n)] for _ in range(len(ans))]
for i,res in enumerate(temp): #第i个答案
for j,row in enumerate(res): #第j个行
row[ans[i][j]]="Q"
temp[i][j]="".join(temp[i][j])
return temp
# 这是个代码片段
# A为答案,cur为第几行下标
def main(n):
ans=[]
def queen(A, cur=0):
if cur == len(A):
ans.append(A[:]) #没写[:]不行,什么机制还不知道
return
for i in range(len(A)):
A[cur] = i
flag = True
#检验与前面的皇后是否冲突
for j in range(cur):
if A[j]==i or abs(i - A[j]) == cur - j:
flag = False
break
if flag: queen(A, cur+1)
queen([None]*n)
return ans
main(8)
(5)解数独
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
def backtrack():
for i in range(9):
for j in range(9):
if board[i][j]!= '.': continue
for num in "123456789":
if check(i,j,num):
board[i][j]=num
if backtrack(): return True
board[i][j]='.'
return False
return True
def check(x,y,num):
for i in range(9):
if board[x][i]==num: return False
if board[i][y]==num: return False
for i in [0,1,2]:
for j in [0,1,2]:
if board[x//3*3+i][y//3*3+j]==num: return False
return True
backtrack()
#回溯,,6
#这种暴力回溯,时间复杂度太高了
#尝试了一下引入参数,回溯不回来了,好菜
(7)131. 分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
class Solution:
def partition(self, s: str) -> List[List[str]]:
ans=[]
def bk(tmp,l,r):
if l==r:
ans.append(tmp[:])
return
for i in range(l+1,r+1):
cur=s[l:i]
if cur==cur[::-1]:
tmp.append(cur)
bk(tmp,i,r)
tmp.pop()
bk([],0,len(s))
return ans
# 后期试错出来的,
# 回溯神奇啊
(8)组合总和 II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
- 所有数字(包括目标数)都是正整数。
- 解集不能包含重复的组合。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
ans=[]
candidates.sort()
def bk(tmp,l,r):
if sum(tmp)==target:
ans.append(tmp[:])
return
if sum(tmp)>target: return
for i in range(l,r):
if i>l and candidates[i]==candidates[i-1]:
continue #这种回溯中去重。。。
tmp.append(candidates[i])
bk(tmp,i+1,r)
tmp.pop()
bk([],0,len(candidates))
return ans
# 记录报错:unhashble type: 'list',列表中列表不能集合去重
# 回溯之前,sort优化,并方便去重
(9)组合总和 III
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
ans=[]
def bk(path,l,k,n):
if n==k==0:
ans.append(path[:])
return
if n<0 or k==0: return
for i in range(l,10):
path.append(i)
bk(path,i+1,k-1,n-i)
path.pop()
bk([],1,k,n)
return ans
# if剪枝 if结束
(10)复原IP地址
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址正好由四个整数(每个整数位于 0 到 255 之间组成),整数之间用 . 分隔。
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
ans=[]
def f(s,tmp):
if len(s)==0 and len(tmp)==4:
ans.append(".".join(tmp))
return
if len(tmp)<4:
for i in range(min(3,len(s))):
head,tail=s[:i+1],s[i+1:]
if head and 0<=int(head)<=255 and str(int(head))==head:
f(tail,tmp+[head])
f(s,[])
return ans
# 一棵递归树
# str(int(i))==i排除前缀0
212. 单词搜索 II
class Trie:
def __init__(self):
self.children = defaultdict(Trie)
self.word = "" # 用于唯一标识
def insert(self, word):
cur = self
for c in word:
cur = cur.children[c]
cur.is_word = True
cur.word = word
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
rows, cols = len(board), len(board[0])
res = set()
trie = Trie()
for word in words:
trie.insert(word)
def dfs(p, i, j):
if board[i][j] not in p.children:
return
c = board[i][j]
p = p.children[c]
if p.word:
res.add(p.word)
p.word = ""
if p.children:
board[i][j] = '#'
for x,y in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:
if 0<=x<rows and 0<=y<cols:
dfs(p, x, y)
board[i][j] = c #回溯
for i in range(rows):
for j in range(cols):
dfs(trie, i, j)
return list(res)
980. 不同路径 III
在二维网格 grid 上,有 4 种类型的方格:
1表示起始方格。且只有一个起始方格。2表示结束方格,且只有一个结束方格。0表示我们可以走过的空方格。-1表示我们无法跨越的障碍。- 返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
class Solution:
def uniquePathsIII(self, grid: List[List[int]]) -> int:
rows, cols = len(grid), len(grid[0])
cnt = 0
for i in range(rows):
for j in range(cols):
if grid[i][j] == 0:
cnt += 1
elif grid[i][j] == 1:
start = (i,j)
def bk(cur, steps):
x, y = cur
if grid[x][y] == 2:
return 1 if steps==0 else 0
ans = 0
for i, j in [(x-1,y),(x+1,y),(x,y-1),(x,y+1)]:
if 0<=i<rows and 0<=j<cols and grid[i][j] != -1:
grid[x][y] = -1
ans += bk((i,j), steps-1)
grid[x][y] = 0 #回溯
return ans
return bk(start, cnt + 1)
