2021春季个人赛

LCP28.采购方案

小力将 N 个零件的报价存于数组 nums。小力预算为 target，假定小力仅购买两个零件，要求购买零件的花费不超过预算，请问他有多少种采购方案。

注意：答案需要以 1e9 + 7 (1000000007) 为底取模，如：计算初始结果为：1000000008，请返回 1

双指针

class Solution:
    def purchasePlans(self, nums: List[int], target: int) -> int:
        n = len(nums)
        nums.sort()
        l, r = 0, n-1
        res = 0
        #print(nums)
        while r>l:
            while r>l and (nums[l]+nums[r]>target):
                r -= 1
            res += r-l
            l += 1
        return res%1000000007

LCP29.乐团站位

某乐团的演出场地可视作 num * num 的二维矩阵 grid（左上角坐标为 [0,0])，每个位置站有一位成员。乐团共有 9 种乐器，乐器编号为 1~9，每位成员持有 1 个乐器。
请返回位于场地坐标 [Xpos,Ypos] 的成员所持乐器编号。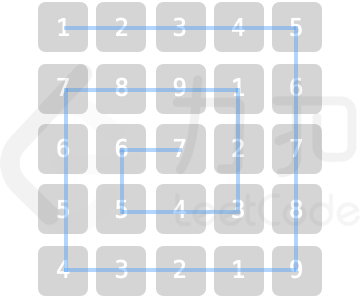

class Solution:
    def orchestraLayout(self, num: int, x: int, y: int) -> int:
        depth = min(x, y, num-x-1, num-y-1)    #位置前面的圈数
        ans = num*num - (num-2*depth)**2       #前面几圈的数
        start, end = depth, num - depth

        if x == depth:            #左边
            ans += y - start
        elif y == depth:          #上边
            ans += (end-start-1)*3 + end - x - 1
        elif x == end - 1:
            ans += (end-start-1)*2 + end - y - 1
        else:
            ans += end-start-1 + x - start

        return ans%9 + 1

#后面还是不懂

LCP30.魔塔游戏

小扣当前位于魔塔游戏第一层，共有 N 个房间，编号为 0 ~ N-1。每个房间的补血道具/怪物对于血量影响记于数组 nums，其中正数表示道具补血数值，即血量增加对应数值；负数表示怪物造成伤害值，即血量减少对应数值；0 表示房间对血量无影响。

小扣初始血量为 1，且无上限。假定小扣原计划按房间编号升序访问所有房间补血/打怪，为保证血量始终为正值，小扣需对房间访问顺序进行调整，每次仅能将一个怪物房间（负数的房间）调整至访问顺序末尾。请返回小扣最少需要调整几次，才能顺利访问所有房间。若调整顺序也无法访问完全部房间，请返回 -1。

from heapq import *
class Solution:
    def magicTower(self, nums: List[int]) -> int:
        if sum(nums) < 0: return -1 
        q = []
        cur = 1
        ans = 0
        for num in nums:
            cur += num
            if num < 0:
                heappush(q, num)
            if cur <= 0:
                cur -= heappop(q)
                ans += 1
        return ans

# 用优先队列存储可以用的梯子

LCP31.变换的迷宫

TLE(35/59)，练了一下DFS

class Solution:
    def escapeMaze(self, maze: List[List[str]]) -> bool:
        self.ans = False
        rows, cols, t = len(maze[0]), len(maze[0][0]), len(maze)

        @lru_cache(None)
        def dfs(x, y, tt, a, b, c):

            # 出口处理
            if x==rows-1 and y==cols-1:
                self.ans = True
                return 
            if tt == t-1:        #最后时刻
                return

            #print(tt,t)
            #方格处理
            grid = []
            for row in maze[tt+1]:
                grid.append([i for i in row])
            #print(grid)
            if c:
                grid[c[0]][c[1]] = "."
            
            #开始暴力
            for (i,j) in [(x-1,y),(x+1,y),(x,y-1),(x,y+1),(x,y)]:  #5个位置
                if 0<=i<rows and 0<=j<cols:  
                    if  grid[i][j] == ".":               #"."直接走         
                        dfs(i, j, tt+1, a, b, c)
                    else:
                        if a:                              #使用临时消除
                            dfs(i, j, tt+1, 0, b, c)
                        if b:                              #使用永久消除
                            dfs(i, j, tt+1, a, 0, (i,j))
                        

        dfs(0, 0, 0, 1, 1, None)
        return self.ans

LCP32.批量处理任务

某实验室计算机待处理任务以 [start,end,period] 格式记于二维数组 tasks，表示完成该任务的时间范围为起始时间 start 至结束时间 end 之间，需要计算机投入 period 的时长，注意：

• period 可为不连续时间
• 首尾时间均包含在内
  处于开机状态的计算机可同时处理任意多个任务，请返回电脑最少开机多久，可处理完所有任务。

提示：

• 2 <= tasks.length <= 10^5
• tasks[i].length == 3
• 0 <= tasks[i][0] <= tasks[i][1] <= 10^9
• 1 <= tasks[i][2] <= tasks[i][1]-tasks[i][0] + 1

class Solution:
    def processTasks(self, tasks: List[List[int]]) -> int:
        tasks.append([10**9+1, 10**9+1, 1])  #哨兵，无法与任何任务维系
        ans, heap = 0, []  #heap表可以维系在一起的任务池
        for s, e, p in sorted(tasks, key = lambda x: x[0]): #按启动时间遍历
            while heap and heap[0][0]+ans < s: #不可维系
                if heap[0][0]+ans >= heap[0][1]: 
                    heappop(heap)
                else:
                    ans+=min(heap[0][1],s)-(heap[0][0]+ans)
            heappush(heap,[e-p+1-ans, e+1])
            #print(heap)
        return ans

#要ans最小，则处于前面的任务开始时间后移

#e-p+1, 为任务最晚启动时间，
#e-p+1-ans, 应该是把前面已用的时间剃掉的，任务最晚启动时间
#e+1, 为任务最晚时间+1

#真难,不懂

#include <bits/stdc++.h>

using namespace std;

#define POW2(X) (1<<(X))
#define CKBIT(S,X) (((S)&POW2(X))!=0)
const double pi=acos(-1.0);
const double eps=1e-11;
template<class T> inline void ckmin(T &a,T b){ a=min(a,b); }
template<class T> inline void ckmax(T &a,T b){ a=max(a,b); }
template<class T> inline T sqr(T x){ return x*x; }
#define SIZE(A) ((int)A.size())
#define LENGTH(A) ((int)A.length())
#define MP(A,B) make_pair(A,B)
#define PB(X) push_back(X)
#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define REP(i,a) for(int i=0;i<(a);++i)
#define ALL(A) A.begin(),A.end()
template<class T> int CMP(T a[],const T b[],int n) { return memcmp(a,b,n*sizeof(T)); }
template<class T> void COPY(T a[],const T b[],int n) { memcpy(a,b,n*sizeof(T)); }
template<class T> void SET(T a[],int val,int n) { memset(a,val,n*sizeof(T)); }
using uint=unsigned int;
using int64=long long;
using uint64=unsigned long long;
using ipair=pair<int,int>;
using VI=vector<int>;
using VD=vector<double>;
using VVI=vector<VI>;
using VS=vector<string>;

class Solution
{
public:
    int processTasks(vector<vector<int>>& tasks) 
    {
        /*
        tasks.clear();
        REP(i,100000)        
        {
            int a=rand();
            int b=rand();
            if (a>b) swap(a,b);
            int c=rand()%(b-a+1)+1;
            tasks.push_back({a,b,c});
        }
        */
        struct Task
        {
            int s;
            int t;
            int length;
        };
        vector<Task> a;
        for (auto t:tasks) 
        {
            Task x;
            x.s=t[0];
            x.t=t[1];
            x.length=t[2];
            a.push_back(x);
        }
        sort(ALL(a),[](const Task& a,const Task& b) {
                return a.t<b.t;
            });
        vector<ipair> segs;
        vector<int> prefix;
        segs.push_back(MP(-1,-2));
        prefix.push_back(0);
        for (Task task:a)
        {
            assert(SIZE(segs)==SIZE(prefix));
            int total=0;
            int s=task.s;
            auto it=lower_bound(ALL(segs),MP(s,-1));
            int at=std::distance(segs.begin(),it);
            total+=prefix.back()-(at==0?0:prefix[at-1]);
            for (int i=at-1;i>=0;i--)
                if (segs[i].second<s)
                    break;
                else if (segs[i].first<=s)
                {
                    total+=segs[i].second-s+1;
                    break;
                }
                else
                    total+=segs[i].second-segs[i].first+1;
            if (total>=task.length) continue;

            total=task.length-total;
            int last=task.t;
            while (1)
            {
                ipair w=segs.back();
                int d=last-w.second;
                if (d<total)
                {
                    total-=d;
                    segs.pop_back();
                    prefix.pop_back();
                    last=w.first-1;
                    continue;
                }
                segs.push_back(MP(last-total+1,task.t));
                int tt=prefix.back()+segs.back().second-segs.back().first+1;
                prefix.push_back(tt);
                break;
            }
        }
        int ret=0;
        for (auto t:segs) ret+=t.second-t.first+1;
        return ret;
    }
};

//小马智行CTO写的...